Counting Ones in a Window
Contents
Counting Ones in a Window#
Suppose we have a bit stream window of length \(N\) and we want to count the number of ones in the last \(k\) bits. Again assume that \(k\) is too large so we cannot afford to store it all \(k\) bits in memory, as would be needed to get an exact count. We can use the Datar-Gionis-Indyk-Motwani (DGIM) algorithm to approximate the count with an error rate of no greater than 50%.
Datar-Gionis-Indyk-Motwani Algorithm#
Assume we have a bit stream window of ‘10101100111011011000101110110010110’. We give each bit a timestamp starting with 1 for the earliest bit, 2 for the 2nd bit, and so on. We divide the bits into buckets consisting of:
The timestamp of its most rightmost (most recent) end.
The number of ones in the bucket. This number must be a power of 2, and we refer to this as the size of the bucket.
Furthermore, the buckets of the bit stream have to follow the following rules:
The right end of a bucket is always a bit with a value 1.
Every bit with a value of 1 is in some bucket.
No bit is in more than one bucket.
There are just one or two buckets of any given size.
All sizes must be a power of 2.
Buckets cannot decrease in size as we move to the left.
Once we’ve split the bit stream into buckets, we can now estimate the number of 1’s for any \(k\) in the window. Find the bucket \(b\) with the earliest timestamp that includes some of the \(k\) most recent bits. The estimate of the number of ones is the sum of the sizes of all buckets to the right of \(b\), plus half the size of \(b\) itself.
For example, take the stream above having the buckets as shown and with \(k=10\). We want to get the count of ones in the 10 rightmost bits, or 0110010110. The bucket with size 4 containing ‘11101’ is the earliest bucket which contains the at least some of last \(k\) bits. We take half the size of this bucket, which equals to 2, plus the sizes of the buckets to the right, so 2, 1, and 1. The DGIM estimate for the number of ones is therefore \(2+2+1+1=6\), which is close to the actual answer of 5.
Let’s try another example, this time counting the ones in the last 20 elements of bit stream …100011101011010001110111101000001010101001000000000100101001100, divided into the following buckets:
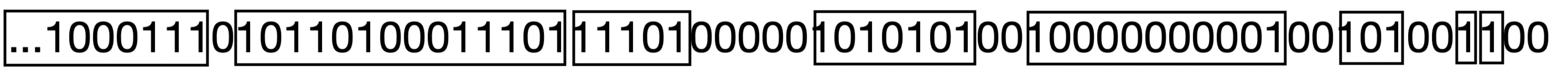
bitStream = '100011101011010001110111101000001010101001000000000100101001100'
k=20 #Count ones in last k=20 elements
buckets = {}
buckets[2] = 1
buckets[3] = 1
buckets[6] = 2
buckets[11] = 2
buckets[24] = 4
buckets[36] = 4
buckets[41] = 8
buckets[56] = 8
earliestBucket = True
approxCount = 0
for ts in sorted(buckets.keys(), reverse=True):
if ts > k:
continue
if earliestBucket:
approxCount += int(buckets[ts] / 2)
earliestBucket = False
else:
approxCount += buckets[ts]
print('Approx Count', approxCount)
realCount = 0
for b in range(k):
if bitStream[-b-1] == '1':
realCount += 1
print('Real Count', realCount)
Updating Buckets with New Data#
When a new data comes in from the stream, we may need to update the buckets in a way that everything will still follow the DGIM conditions. When a new bit enters, we take the following steps:
Check the leftmost bucket. If the timestamp has has gone past the our window of length \(N\),remove it from the list of buckets we are tracking.
If the new bit is 0, we do not need to do anything.
If the new bit is 1, we first create a new bucket of size 1 containing the new bit. If there was only one bucket of size 1, then nothing more needs to be done.
If there are now 3 buckets of size 1, we combine the 2 leftmost buckets of size into one bucket of size 2.
Do step #4 repeatedly for the buckets with sizes greater than 1 until all the buckets follow the DGIM rules once again.
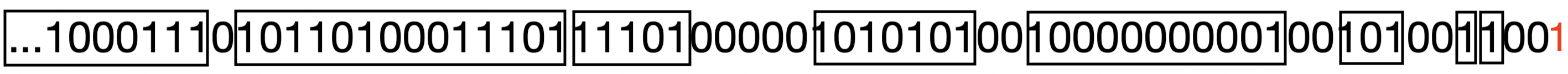
N = 60
#Existing bucket groupings
buckets = {}
buckets[2] = 1
buckets[3] = 1
buckets[6] = 2
buckets[11] = 2
buckets[24] = 4
buckets[36] = 4
buckets[41] = 8
buckets[56] = 8
for key in sorted(buckets.keys(), reverse=True): #add all existing buckets back with their rightmost index incremented by 1
if key+1 > N: #No need to add if bucket is now out of window
continue
buckets[key+1] = buckets[key]
del buckets[key]
buckets[0] = 1 #create a new bucket of size 1 containing the new bit
for size in [1,2,4,8,16]:
buckets_ = [k for k,v in buckets.items() if v==size]
if len(buckets_) > 2:
max_bucket = max(buckets_)
buckets[max_bucket] = size*2
continue
sizeCount = 0
sizeIndexes = []
for key in sorted(buckets.keys()):
if buckets[key] == size:
sizeCount += 1
sizeIndexes.append(key)
elif buckets[key] > size:
break
#Only need to do something if more than 2 buckets have the same size
if sizeCount > 2:
newSize = size * 2
#combine the 2 leftmost buckets of the same size into one bucket of twice the size.
buckets[sizeIndexes[1]] = newSize
del buckets[sizeIndexes[2]]
print(buckets)
{57: 16, 42: 8, 37: 8, 25: 4, 12: 4, 7: 2, 4: 2, 3: 1, 0: 1}
Error Bounds#
Suppose that the exact count is \(c\), and the DGIM estimate involves a leftmost bucket \(b\) of size \(2^j\). We consider 2 error cases separately, one where the estimate is larger than \(c\) and one where the estimate is smaller than \(c\).
The estimate is smaller than \(c\). The worst case scenario is all the 1’s in \(b\) should have been part of the count, and using only \(\frac{1}{2}\) of the size of \(b\) only gives us \(2^{j-1}\) 1’s. However \(c\) should be at least \(2^{j+1}-1\). Thereforce we conclude that our estimate is at least 50% of \(c\).
The estimate is larger than \(c\). The worst case scenario is only the rightmost bit of bucket \(b\) is included, and there is only one bucket of each of the sizes smaller than \(b\). Then \(c = 1+2^{j−1} +2^{j−2} +···+1=2^j\), and the estimate we get from DGIM is \(2^{j−1} + 2^{j−1} + 2^{j−2} + · · · + 1 = 2^j + 2^{j−1} − 1\). Therefor we can conclude that the estimate is no more than 50% greater of \(c\).
We can improve the error bounds further by replacing the condition that there can only be 1 or 2 buckets for each size, with instead there being \(r\) or \(r-1\) buckets for each size with \(r > 2\).
Exercise#
What would be the placements of buckets for bit stream “011100010101110000110110110” ?