Set Similarity

When we are given a dataset of documents, which can be news articles, webpages, item descriptions, and we are asked to determine how similar these documents are, the naive approach is to compare each possible pair then compute for the similarity of each pair. However, as we may guess, this approach is quite expensive as it requires looking at all pairs.

This would mean that for a given \(N\) document, looking at all the pairs would take roughly \(O(N^2)\) time (Equation \ref{brute-force}):

\[ \frac{N!}{2! (N - 2)!} \sim N^2/2 \sim O(N^2) \tag{1} \label{brute-force} \]

Throughout this chapter, we will discuss one way we can approximate the computation of this simlarity through the use of hashing functions, specifically, Locality-Sensitive Hashing (LSH), which allows us to focus on pairs that are likely to be similar without looking at all the pairs. These fucntions are built to contain property that pairs that are more similar tend to be on the same bucket defined by the hash functions.

To build our understanding of LSH, we first need to define a metric that allows us to evaluate the similarity of the pairs of items. In this section, we discuss the notion of the Jaccard Similarity of sets, as this will be the basis in which we will define our LSH. Such LSH define in this metric is called Minhash functions which we will discuss in Section 3 of this Chapter.

Jaccard Similarity of Sets

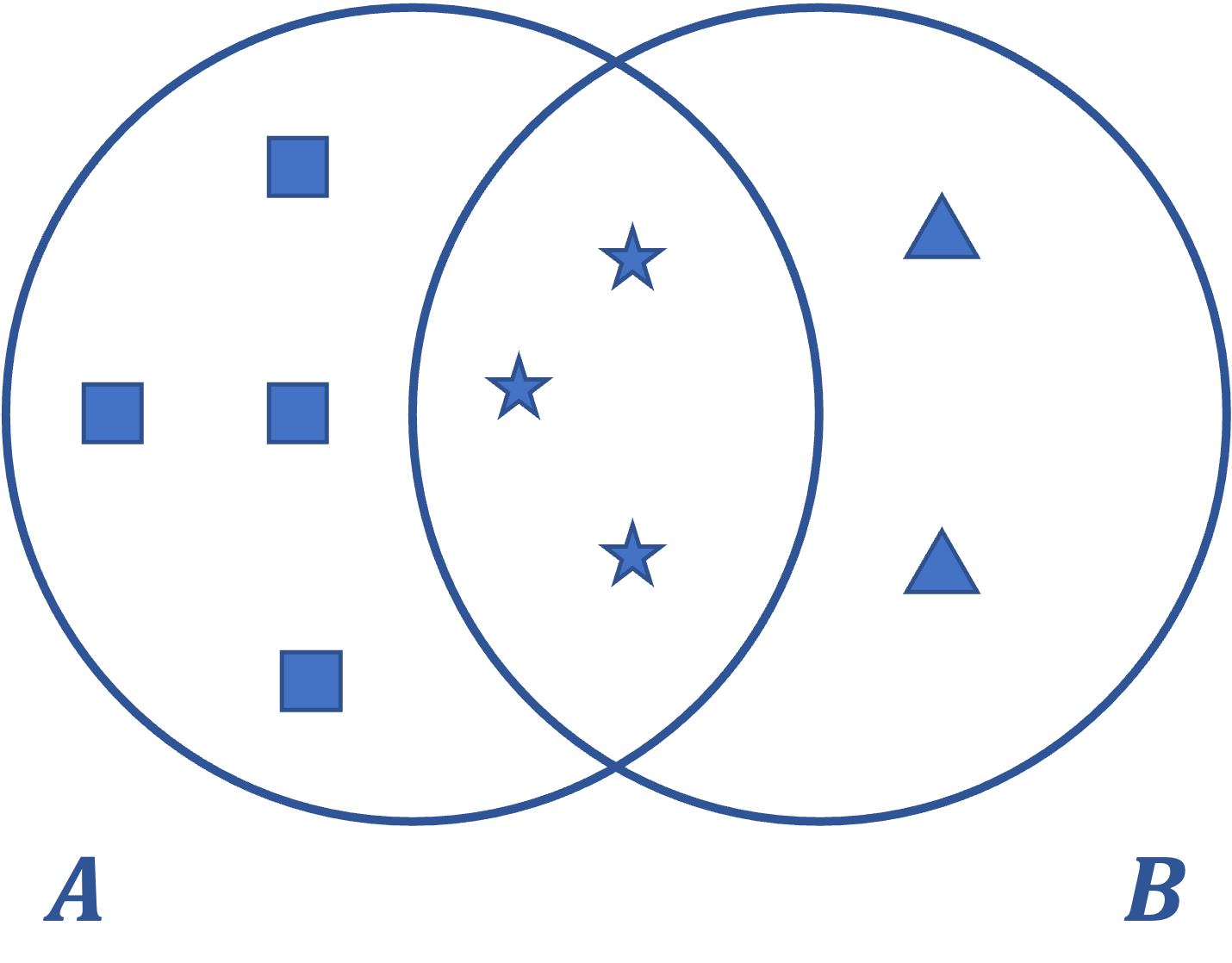
Fig. 2 Two sets A and B having a Jaccard similarity of 3/9.

Jaccard Similarity is a metric defined as the similarity of the sets in relation to the size of their intersection (See Fig. 2).

Mathematically, if we are given two sets \(A\) and \(B\), the Jaccard Similarity which we denote as \(SIM(A, B)\) is given by:

\[ SIM(A, B) = \frac{|A \cap B |}{| A \cup B |} \tag{2} \]

Example 1: Calculating the Jaccard Similarity of two sets

Two movie goers have watch the following shows:

Leo = {'Detachment (2011)', 'Hotel Transylvania (2012)', 'Interstellar (2014)', 'The Godfather (1972)'}
Mike = {'Interstellar (2014)', 'Hotel Transylvania (2012)', 'October Sky (1999)', 'American Beauty (1999)'}

Compute for the Jaccard Similarity of these two users.

Solution

Let us denote \(L\) and \(M\) as the movies that Leo and Mike watched respectively. Mathematically, we can compute for the intersection and union of each sets as:

\[\begin{split} L \cap M = \text{{'Interstellar (2014)', 'Hotel Transylvania (2012)'}} \\ L \cup M = \text{{'Interstellar (2014)', 'Hotel Transylvania (2012)', 'October Sky (1999)', 'American Beauty (1999)', 'Detachment (2011)', 'The Godfather (1972)'}} \end{split}\]

Afterwards, verifying that the length of intersection between the two set is 2, while the length of the union of the two sets is 6, we get the Jaccard Similarity as:

\[ SIM(L, M) = \frac{2}{6} = \frac{1}{3} \]

We can also solve the problem using Python. First we define the two sets:

L = {'Detachment (2011)', 'Hotel Transylvania (2012)', 'Interstellar (2014)',
     'The Godfather (1972)'}
M = {'Interstellar (2014)', 'Hotel Transylvania (2012)', 'October Sky (1999)',
     'American Beauty (1999)'}

Then compute the length of their intersection nad length of their union.

intersection_length = len(L.intersection(M))
union_length = len(L.union(M))

jaccard_LM = intersection_length / union_length

print(f"The Jaccard Similarity of L and M is {jaccard_LM:.3f}")

The Jaccard Similarity of L and M is 0.333

Characteristic Matrix Representation

We may also represent the sets \(L\) and \(M\) and all the movie items in the universe as a characteristic matrix. Here, the columns of the matrix corresponds to the sets, and the rows corresponds to the elements of the universal sets. In this representation, the \(L\) and \(M\) sets chosen from the universal set of {I, HT, OS, AB, D, TG} may be written as:

	L	M
I	1	1
HT	1	1
OS	0	1
AB	0	1
D	1	0
TG	1	0

We leave it as an exercise for the reader for them how to define the jaccard similarity given a characteristic matrix representation. However, using the alis API function jaccard_sim() from the alis.similarity module, this can be done as follows:

import numpy as np

from alis.similarity import jaccard_sim

characteristic_matrix = np.array(
    [[1, 1],
     [1, 1],
     [0, 1],
     [0, 1],
     [1, 0],
     [1, 0]])

jaccard_sim(characteristic_matrix, 0, 1)

0.33333333333333337

We get the same result as what we previously computed earlier mathematically and using set operations.

Exercises

Exercise 1

Compute for the Jaccard similarity between each pair of the following sets:

L = {'A', 'B', 'C', 'D', 'E'}
M = {'B', 'C', 'F', 'G', 'H'}
N = {'F', 'H', 'A', 'B'}

Try to construct the characteristic matrix of the above sets along with the universal items then use the jaccard_sim function to easily compute the Jaccard similarity of each pairs.