Topic-Sensitive PageRank#

The PageRank algorithm could be modified so that it can put more weight to certain pages depending on some topic. One possible motivation for this is to make search results more relevant to the user. The Topic-Sensitive PageRank creates a vector for a set of topics with the goal of giving bias to these topics. Obviously, the ideal case would be to create one vector per user, but this is simply not possible. Having vectors for only a number of topics, while more limited, can still provide more relevant search results.

Deciding on the topic set is the first step in implementing Topic-Sensitive PageRank. One such possible set is the top-level categories of the Open Directory: Arts, Business, Computers, etc.

We have saved the functions we have defined in the previous sections in a module called link_analysis. We import that module below, together with numpy.

import numpy as np
from alis import link_analysis

Description#

The implementation of Topic-Sensitive PageRank is similar to the general PageRank, except that teleports only happen to a predefined teleport set consisting of pages from a specific topic.

Given

  • \(S\) - the indices of the pages belonging to the teleport set

  • \(|S|\) - the size of the teleport set

  • \(\textbf{e}_s\) - vector such that

    \( {\large \textbf{e}_{s_{i}}}=\left\{ \begin{array}{@{}ll@{}} 1, & \text{if } i \text{ is in } S \\ 0, & \text{otherwise} \end{array}\right. \)

Then, the topic-sensitive PageRank for \(S\) is the limit of the following iteration:

\[ \textbf{v'}= \beta M\textbf{v} + (1-\beta)\textbf{e}_s/|S| \]

Implementation#

We implement below the algorithm just described:

def topic_sensitive_page_rank(M, S, beta=0.8, tol=10**-6, max_iter=100):
    """Compute the topic-sensitive PageRank (with taxation) of a given Transition Matrix 

    Parameters
    ----------
    M : numpy array
        Transition Matrix: Array of shape (n, n), where n is the number
        of nodes in the network
    beta :  float
        probability of following an outlink
    S :  list
        indices of pages belonging to the teleport set
        (indices start at 0)
    tol : float
        Tolerance: Iteration stops if the distance between previous and
        updated PageRank vectors goes below this value
    max_iter : integer
        Maximum number of iterations
    Returns
    -------
    v : numpy array
        Vector of size n containing the PageRank values 
    """
    
    n = M.shape[0]
    e = np.zeros(n)
    for i in S:
        e[i] = 1
        
    v = np.ones(n)
    delta = 1/tol # initialize to a large number
    i = 0
    while delta > tol:
        i += 1
        prev_v = v
        v = beta*M.dot(v) + ((1-beta)/len(S))*e
        delta = np.mean(np.abs(v-prev_v))
        if i >= max_iter:
            break        
    return v

To illustrate, recall Graph 1:

import networkx as nx
import matplotlib.pyplot as plt

G1 = nx.DiGraph()
G1.add_nodes_from(["A","B","C","D","E"])
G1.add_edges_from([
    ("A","B"), ("A","C"), ("A","D"), ("A","E"), 
    ("B","A"), ("B","D"), 
    ("C","A"),    
    ("D","B"), ("D","C"),
    ("E","B"),
])

plt.figure()  
plt.title("Graph 1. A Graph as a hypothetical representation of the web")
nx.draw(G1, node_size=500, node_color='orange', with_labels=True,
        font_weight='bold', arrowsize=20)
plt.tight_layout()
plt.show()
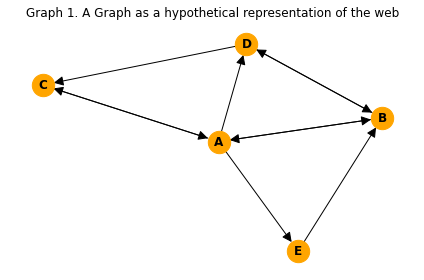
../_images/topic-sensitive-pagerank_10_0.png

Assuming that pages B and D are our teleport set, we can implement the Topic-Sensitive PageRank in Graph1 as follows:

S = [1,3]
M = link_analysis.transition_matrix(G1)
topic_sensitive_page_rank(M,S)

array([0.24028021, 0.29252947, 0.15408413, 0.26506858, 0.04805632])

Using Topic-Sensitive PageRank in a search engine#

Topic-Sensitive PageRank can be used by a search engine following the steps below:

  1. Choose a set of topics

  2. Decide on a teleport set for each topic

  3. Given a query, find the most relevant topic

  4. Use the corresponding teleport set in calculating the topic-sensitive PageRank

TrustRank#

TrustRank is a variation of the Topic-Sensitive PageRank where the ‘topic’ that defines the teleport set is a set of pages that are believed to be trustworthy.

A feasible way of selecting the trustworthy pages is to pick a domain whose membership is controlled. Examples are .edu, .gov, .mil.

Spam Mass#

The idea of Spam Mass is to deduct PageRank scores from pages which are considered spam. This can be done by calculating both the PageRank score and the TrustRank score.

Given

  • \(r\) - PageRank of a page

  • \(t\) - TrustRank of the same page

The page’s spam mass \(p\) is calculated as follows:

\[ p = (r-t)/r \]

Below is an implementation of spam mass which calls the idealized_page_rank and topic_sensitive_page_rank functions from our link_analysis module.

def spam_mass(M, S, beta=0.8, tol=10**-6, max_iter=100):
    """Compute the spam mass given a set of trustworthy pages

    Parameters
    ----------
    M : numpy array
        Transition Matrix: Array of shape (n, n), where n is the number
        of nodes in the network
    beta :  float
        probability of following an outlink; passed to page_rank_ts
    S :  list
        indices of trustworthy pages (indices start at 0)
    tol : float
        Tolerance: Iteration stops if the distance between previous and
        updated PageRank vectors goes below this value
    max_iter : integer
        Maximum number of iterations
    Returns
    -------
    p : numpy array
        Vector containing the spam mass 
    """
    r = link_analysis.idealized_page_rank(M, tol=tol, max_iter=max_iter)
    t = link_analysis.topic_sensitive_page_rank(
        M, S=S, beta=beta, tol=tol, max_iter=max_iter)
    p = (r-t)/r
    return p

Let’s check the spam mass of Graph1 if nodes B and D are in the teleport set.

spam_mass(M, [1, 3])

array([ 0.19906599, -0.17011728,  0.11951934, -0.32534358,  0.35924862])

REFERENCE [LRU20]