Hubs and Authorities
Contents
Hubs and Authorities#
Another method for analyzing the importance of web pages is Hubs and Authorities, also known as HITS (Hyperlink-Induced Topic Search), proposed shortly after PageRank was implemented. This section describes how this method is implemented.
The Link Matrix#
The HITS algorithm also makes use of a matrix to compute the score of ‘hubbiness’ or authority of pages. Let’s assume that these scores are represented by the vectors \(\textbf{h}\) and \(\textbf{a}\). Further assume that \(n\) is the number of pages in the network.
To compute \(\textbf{h}\) and \(\textbf{a}\), we need a matrix to contain information about the links. For the HITS algorithm, this matrix is called the link matrix \(L\), of size \(n\) x \(n\).
If we denote the elements of \(L\) as \(\ell_{ij}\), we have:
\( \ell_{ij}=\left\{ \begin{array}{@{}ll@{}} 1, & \text{if there is a link from page } i \text{ to } j \\ 0, & \text{otherwise} \end{array}\right. \)
Note that, compared to the Transition Matrix of PageRank, the direction for putting entries in the matrix is reversed, since for the transition matrix, the entries are defined according to links from \(j\) to \(i\). Aside from the matrix \(L\), hits also makes use of its transpose, \(L^T\). Note that \(L^T\) is similar to the transition matrix, only that its entries are \(1\) for instead of \(1/n\) for the non-zero elements.
Given the earlier discussion on graph notations, we observe that the Link Matrix is actually nothing but the adjacency matrix of the graph.
import networkx as nx
import matplotlib.pyplot as plt
G4 = nx.DiGraph()
G4.add_nodes_from(["A","B","C","D","E"])
G4.add_edges_from([
("A","B"), ("A","C"), ("A","D"),
("B","A"), ("B","D"),
("C","E"),
("D","B"), ("D","C")
])
plt.figure()
plt.title("Graph 4. A sample graph for illustrating the HITS algorithm")
nx.draw(G4, node_size=500, node_color='orange', with_labels=True, font_weight='bold', arrowsize=20)
plt.tight_layout()
plt.show()
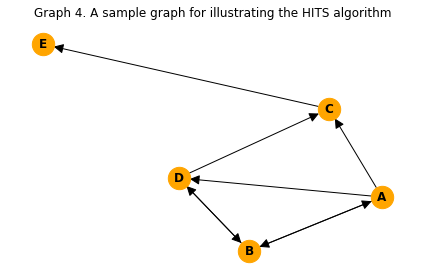
The link matrix or adjacency matrix of \(G4\) is given by:
nx.adjacency_matrix(G4).toarray()
array([[0, 1, 1, 1, 0],
[1, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 1, 1, 0, 0],
[0, 0, 0, 0, 0]])
Deriving the HITS update rule#
Recall in PageRank that the score of a page is distributed to its successors. In the case of HITS, the score passed to the successors. In order to prevent values from growing without bounds, the values are normally scaled so that the largest value of a component is 1.
Given constants \(\lambda\) and \(\mu\) to represent the scaling factor, we can describe the iteration step for updating \(\textbf{h}\) and \(\textbf{a}\) as follows:
\(\textbf{h'} = \lambda L \textbf{a} \)
\(\textbf{a'} = \mu L^T \textbf{h} \)
Since the hubbiness of a page is proportional to the authority of its successors, and the authority of a page is proportional to the hubbiness of its predecessors, we can actually compute for hubbiness independently, giving us a form that allows us to compute the two values independently.
\(\textbf{h'} = \lambda \mu L L^{T} \textbf{a} \)
\(\textbf{a'} = \lambda \mu L^T L \textbf{h} \)
However, since \(L L^{T}\) and \(L^{T} L\) are not sparse, it is actually better to compute \(\textbf{h}\) and \(\textbf{a}\) recursively. We outline method in the next subsection.
HITS Algorithm#
We can summarize the HITS algorithm as follows:
Initialize \(\textbf{h}\) and \(\textbf{a}\) to a vectors of 1’s (of size \(n\))
Iterate:
Compute \(\textbf{a} = \mu L^T \textbf{h} \)
Scale \(\textbf{a}\) so that the largest component is 1 (i.e., divide each element by the maximum value.)
Compute \(\textbf{h} = \mu L^T \textbf{a} \)
Scale \(\textbf{h}\) so that the largest component is 1
Until changes to \(\textbf{h}\) and \(\textbf{a}\) are sufficiently small.
We implement the hits algorithm below.
def hits(L, tol=10**-6, max_iter=100):
"""Compute the PageRank of a given Transition Matrix
Parameters
----------
L : numpy array
Link Matrix: Array of shape (n, n), where n is the number of nodes in the network
tol : float
Tolerance: Iteration stops if the distance between previous and updated PageRank vectors
goes below this value
max_iter : integer
Maximum number of iterations
Returns
-------
h, a : tuple of numpy array
Vectors of size n containing the hub and authority values
"""
h = np.ones(L.shape[0])
a = np.ones(L.shape[0])
delta = 1/tol # initialize to a large number
i = 0
while delta > tol:
i += 1
# save old values
prev_h = h
prev_a = a
# update a
a = L.T.dot(h)
# scale a
a = a/np.max(a)
# update h
h = L.dot(a)
# scale h
h = h/np.max(h)
delta = np.mean([
np.sum(np.abs(h-prev_h)),
np.sum(np.abs(a-prev_a))
])
if i >= max_iter:
break
return h, a
import numpy as np
L = nx.adjacency_matrix(G4).toarray()
h, a = hits(L)
print(f'h: {h}')
print(f'a: {a}')
h: [1.00000000e+00 3.58257838e-01 1.02588408e-11 7.16515005e-01
0.00000000e+00]
a: [2.08712567e-01 1.00000000e+00 1.00000000e+00 7.91288371e-01
2.86353830e-11]
EXERCISES
Identify pages that can be considered as examples of hubs and authorities
Calculate the \(h\) and \(a\) scores for Graph 1 in the previous section.
REFERENCE [LRU20]