Minhashing
Contents
Minhashing#
The core problem of storing shingles is that they can be too large. One way to circumvent this problem is to replace the large sets required by this shingles into smaller representations thorugh the use of signatures.
One property of signatures should have is that it should be able to compare two different documents and be able to calculate the Jaccard similarity using those signature alone. Although it would be hard to give the exact similarity of the sets, if we can provide an estimate that is close enough, it would suit our use-case. Another quality that we would like is that if we make our signature larger, the more accurate should the estimate be.
Minhash Signatures#
We designate the minhash of a characteristic matrix as the signature for each documents which is a result of a large number of hash calculations. To obtain the minhash of a set, we first permute the rows of the characteristic matrix, then, designate the minhash value of the column as the number of the first row (after permutation), wherein the column has a value of \(1\).
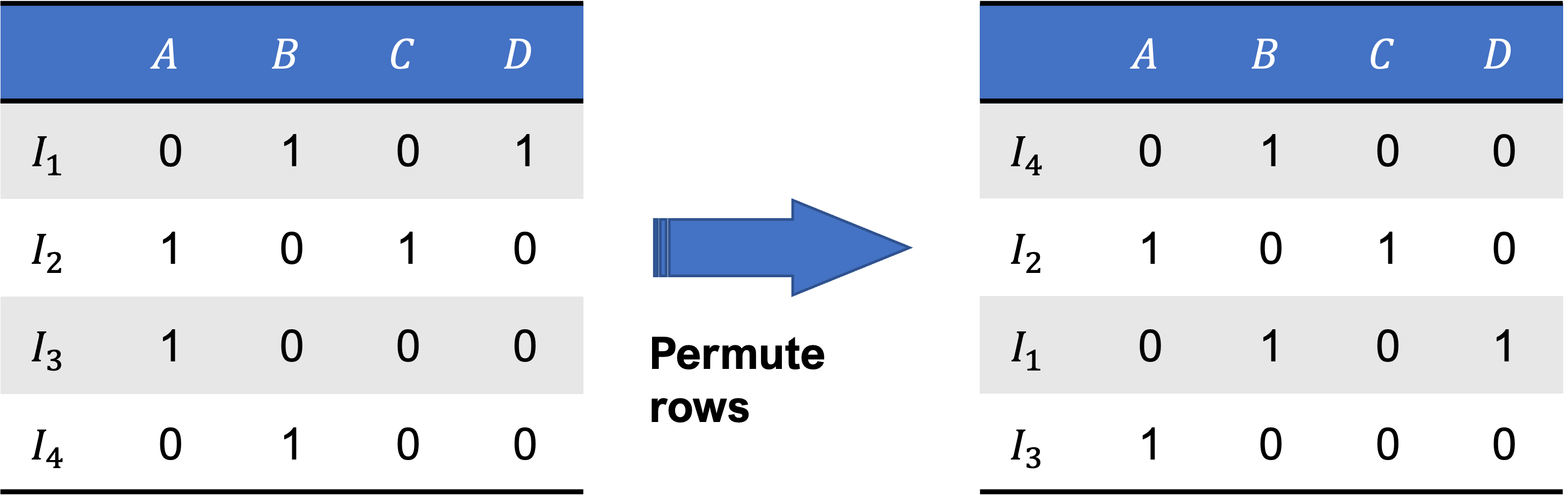
Fig. 4 Computing the minhash value entails permuting the rows then finding the first row in which the column has a 1.#
Say a given minhash function \(h\) permutes the rows of a characteristic matrix according to Fig. 4. In this case, the minhash value of \(A\) is given by \(h(A) = I_2\). For \(B\), since the first row is \(I_4\), it follows that \(h(B) = I_4\). For \(C\), we also get \(h(C) = I_2\), and finally for \(D\), \(h(D) = I_1\).
Minhash and Jaccard Similarity#
The Minhash signature will only be useful if we can use it to compare two different documents and estimate their similarity from the obtained signatures. The connection between the minhash of a document and Jaccard similarity becomes clear from the following theorem [RU11]:
The probability that the minhash function for a random permutation of rows produces the same value for two sets equals the Jaccard similarity
To prove this theorem, consider two sets \(S_1\) and \(S_2\), the rows can either be any of the three types:
Type \(X\) rows have \(1\) in both columns
Type \(Y\) rows have \(1\) in one of the columns and \(0\) in the other
Type \(Z\) rows have \(0\) in both columns
Since the characteristic matrix is expected to be sparse, most of the rows will be of type \(Z\). However, the ration of the type \(X\) and type \(Y\) rows will determine the similarity of the documents \(SIM(S_1, S_2)\) as well as the probability that \(h(S_1) = h(S_2)\).
We can show this by letting \(x\) be the type number of rows of type \(X\), while \(y\) be the number of rows of type \(Y\). Given this, the Jaccard similarity then is equal to:
Since \(x\) will be the size of \(S_1 \cap S_2\) and \(x + y\) will be the size of \(S_1 \cup S_2\).
To prove now that the probability that \(h(S_1) = h(S_2)\) will be equivalent of the above expression. Consider the case where we permute the rows randomly and proceed from the top, the probability that we shall meet a type \(X\) row before we meet a type \(Y\) row. This probability will be equal to \(\frac{x}{x + y}\). But if the first row from the top other than type \(Z\) rows is a type \(X\) row, then we definitely get \(h(S_1) = h(S_2)\). If the first row that we meet is a type \(Y\) row, then the set with \(1\) gets teh row as its minhash value.
Therefore, we see that when we get \(h(S_1) \neq h(S_2)\), we meet a type \(Y\) row. As such, we can conclude that the probability that \(h(S_1) = h(S_2)\) is \(\frac{x}{x + y}\) which is equivalent of the Jaccard similarity of \(S_1\) and \(S_2\).
Computing Minhash Signatures#
To create minhash signatures, we consider a series of minhash functions \(h_1, h_2, ..., h_n\). Each of these minhash functions generates different permutations of the rows of the characteristic matrix. Thus, for each set \(S\), the minhash signature is the vector \([h_1(S), h_2(S), ..., h_n(S)]\). We may therefore represent the signature of a characteristic matrix \(M\) to be a matrix with the same number of columns, where each column represent the set in the matrix, but the rows may be replaced by the minhash signature for the set in the \(i\)-th column.
One challenge in creating minhash signatures is that it is usually not feasuible to permute a large characteristic matrix explicity. As such, we may simulate the effect of random permutations by using a random minhash function taht maps row numbers to as many buckets as there are rows.
Note: Universal Hashing
One effective means for generating hashes is as follows: generate two random numbers \(a\) and \(b\) in the interval \([0, D)\), and return the value of \(hash(x) = (ax + b) mod D\)
Algorithm for Generating Minhash Signatures#
Now we can proceed to define the algorithm for generating minhash signatures.
First, we pick \(n\) random hash functions \(h_1, h_2, ..., h_N\). Then, construct the signature matrix by considering each row based on their given order. We then let \(SIG(i, c)\) be the signature element for the \(i\)-th hash function and column \(c\).
At the start, we initialize all the signature values \(SIG(i, c)\) to be \(\infty\) for all \(i\) and \(c\). We then iterate through each row \(r\) in the characteristic matrix as follows:
Compute \(h_1(r), h_2(r), ..., h_n(r)\).
If \(c\) has \(0\) in row \(r\), do nothing.
However, if \(c\) has \(1\) in row \(r\), then for each \(i = 1, 2, 3, ..., n\), set \(SIG(i, c)\) to the smaller of the current value of \(SIG(i, c)\) and \(h_i(r)\).
Example 1#
Note: This example is taken from [RU11].
Consider the characteristic matrix given by
Row |
S1 |
S2 |
S3 |
S4 |
|---|---|---|---|---|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
1 |
0 |
1 |
3 |
1 |
0 |
1 |
1 |
4 |
0 |
0 |
1 |
0 |
Then we choose two hash functions:
Compute for the minhash signature of this characteristic matrix given the two minhash function defined above.
Solution#
Step 1: We initialize the signature matrix to contain all \(\infty\)
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
∞ |
∞ |
∞ |
∞ |
h2 |
∞ |
∞ |
∞ |
∞ |
Step 2: Iterate through rows of the characteristic matrix
For row 0
Values of both \(h_1(0)\) and \(h_2(0)\) are both \(1\). While only sets \(S_1\) and \(S_4\) have the \(1\)s in row \(0\). Since \(1\) is less than \(\infty\), we change the values in the columns for \(S_1\) and \(S_4\).
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
1 |
∞ |
∞ |
1 |
h2 |
1 |
∞ |
∞ |
1 |
For row 1
The hash values are \(h_1(1) = 2\) and \(h_2(1) = 4\). Only \(S_3\) has \(1\) in this row. Thus we set the values in column \(S_3\) as \(2\) and \(4\) successively.
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
1 |
∞ |
2 |
1 |
h2 |
1 |
∞ |
4 |
1 |
For row 2
The hash values are \(h_1(2) = 3\) and \(h_2(2) = 2\). \(S_2\) and \(S_4\) has \(1\) in this row. However, at \(S_4\) \(3\) and \(2\) are higher than \(1\). Thus we only set \(3\) and \(2\) to the rows of \(S_2\).
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
1 |
3 |
2 |
1 |
h2 |
1 |
2 |
4 |
1 |
For row 3
The hash values are \(h_1(3) = 4\) and \(h_2(3) = 0\). Only \(S_2\) has no \(1\) in this row. However, the current \(h_1\) values for all the other sets are less than \(4\). Thus we only change their \(h_2\) values.
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
1 |
3 |
2 |
1 |
h2 |
0 |
2 |
0 |
0 |
For row 4
The hash values are \(h_1(4) = 0\) and \(h_2(4) = 3\). Only \(S_3\) has \(1\) in this row. However, the current \(h_2\) value for \(S_3\) is less than \(3\). Thus we only change their \(h_1\) value as \(0\).
S1 |
S2 |
S3 |
S4 |
|
|---|---|---|---|---|
h1 |
1 |
3 |
0 |
1 |
h2 |
0 |
2 |
0 |
0 |
Afterwards, we can then use this signature matrix to estimate the Jaccard similarities of the underlying sets.
For example the estimated \(SIM(S_1, S_4) = 1\), while the true Jaccard similairty is \(2/3\).
For \(S_1\) and \(S_3\), the signature columns agree half in the rows (true similarity is 1/4). While the signature of \(S_1\) and \(S_2\) estimate 0 as their Jaccard similarity (same as true value).
Applying Shingling and Minhashing on a Real-World Dataset#
Now, let’s put our study into practice by applying shingling and minhashing on a real-world dataset. We will take the News Group Dataset in sklearn and use dask to perform shingling and minhashing.
We load the dataset using the code below.
from sklearn.datasets import fetch_20newsgroups
# Load the news group dataset without the headers, footers and quotes
newsgroup = fetch_20newsgroups(
subset='train', remove=('headers', 'footers', 'quotes'))
newsgroup_data = newsgroup['data']
Afterwards, let’s initialize our dask client.
from dask.distributed import Client
import dask.bag as db
client = Client()
We load the newsgroup dataset as a dask bag using the from_sequence() function. Note also here that we use the first item in the tuple as an identifier of the text. This enables us to refer to it when we want to compare similar documents. This can also be in the form of filepath for each read documents or hyperlink for scraped urls.
newsgroup_bag = db.from_sequence(
zip(range(len(newsgroup_data)), newsgroup_data))
We define a simple cleaning step by normalizing all the blank space characters into a single space and removing all alpha-numeric characters. We also case normalize the input text for simplicity.
import re
def clean_text(text):
"""Clean text by removing non-alphanumeric characters and replacing
all blank space characters into a single space
"""
return (re.sub(r'\s', r' ', re.sub(r'[^\w\s]', r'', text)).lower())
newsgroup_bag_cleaned = newsgroup_bag.map(lambda x: (x[0], clean_text(x[1])))
We then use the MinhashLSH from alis.feature_extraction API. This allows us to perform word shingling and extract the minhash signatures by just specifying our desired parameters.
from alis.feature_extraction import MinhashLSH
Here, we take the 3-word shingle and set the size of the hash buckets to be between the range of \(0\) and \(2^{12}\). Furthermore, we set the number of hash functions we use for the signatures to be \(10\), and the hash size to be roughly the same size as the range of the hashed word shingles.
minhasher = MinhashLSH(shingle_size=3, num_shingle_bucket=12, num_hash=10,
hash_size=2**12)
We then use the transform() method of our minhasher to get the minhash signature.
newsgroup_signatures = minhasher.transform(newsgroup_bag_cleaned)
Verify that we get now the minhash signatures of each document in our dask bag. After this, we can proceed to take the Jaccard similarity using the signatures to compare the similarity between each document.
newsgroup_signatures.take(10)
((0, [164, 41, 5, 141, 19, 109, 71, 3, 82, 11]),
(1, [285, 41, 15, 141, 230, 16, 8, 3, 89, 35]),
(2, [31, 41, 0, 26, 24, 52, 8, 3, 63, 5]),
(3, [95, 1238, 1095, 487, 858, 700, 737, 129, 214, 1402]),
(4, [94, 293, 145, 266, 484, 208, 134, 66, 136, 10]),
(5, [45, 104, 300, 119, 85, 25, 71, 3, 59, 25]),
(6, [131, 293, 25, 9, 6, 88, 98, 570, 202, 61]),
(7, [128, 41, 0, 31, 6, 40, 17, 3, 42, 3]),
(8, [530, 104, 110, 380, 124, 172, 521, 192, 89, 171]),
(9, [90, 41, 30, 3, 42, 151, 17, 3, 7, 28]))